Set #6 Homework Solutions
Astronomy 1
DUE MONDAY OCTOBER 19
--------------------------
Chapter #3
Probs 4, 6, 10
-------------------
Chapter #4
Probs 2, 5, 8, 10
====================
3-4
Body A blackbody emission peaks at 200 nm.
Body B blackbody emission peaks at 650 nm.
(a)How many times hotter is body A than body B?
(b)How many times more energy per area per second does A radiate
than does body B?
(a) Wein's Law says that Teff proportion to 1/(peak wavelength)
So TA/TB = (wavelength B)/(wavelength A)
and TA/TB = 650 nm / 200 nm = 3.25
Body A is 3-1/4 times hotter than body B
(b) Stephan's Law says that the Power per area radiated is proportional
to the fourth power of the temperature, so:
IA/IB = (TA/TB)4
IA/IB = (3.25)4 = 112
Body A radiates 112 times the radiation that body B does.
---------------------------
3-6
The Sun has an effective surface temperature of 5800 K and its peak
blackbody radiation is at 550 nm. Using this data, determine the peak
wavelength that at protostar with surface temperature of 1000 k radiates.
As in the previous problem
TSun/Tstar = (wavelength star)/(wavelength Sun)
So (wavelength star)/(wavelength Sun) = (5800 K)/(1000 K)
wavelength star = 550 nm (5.8) = 3190 nm
It radiates in the infrared
---------------------------
3-10
A spacecraft in circular orbit about a planet emits radio waves as seen from stationary
observer. The orbit radius is 100,000 km and the maximum and minimum frequencies
observed are 3.00036 m and 2.99964 m.
Find the mass of the planet assuming that the spacecraft is
broadcasting at a constant frequency.
If we can determine the velocity of the spacecraft, we can calculate
the period of the orbit and since we know the radius of the orbit,
we can use Kepler's 3rd Law (as modified by Newton) to calculate
the mass of the planet!!!
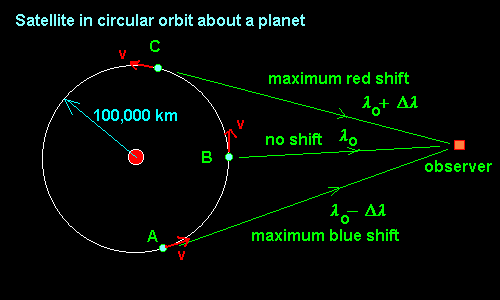 -
The wavelength at which the spacecraft is radiating is the average of the
extremes lo = (lred + lblue)/2 as can be
seen from the fact that lred = lo + dl and lblue = lo - dl
Where l = wavelength
dl = diffence in wavelength = apparent wavelength - actual wavelength
lo = 3.000000 m and then dl = 0.00036 m
Using the doppler effect, we can find the velocity of the spacecraft.
v/c = dl/lo
v = 300,000 km/s (0.00036 m/3 m) = 36 km/s
-
The period of the spacecraft orbit is determined from
time (period) = circumference / speed
period = 2 (pi) r /v = 6.28 (100,000 km) / 36 km/s
period = 17453 s = 4.84 hours = 0.202 days
Since this period is more similar to a satellite about the Earth,
let's use the Earth-Moon for Comparison and we will get the mass
of the planet in terms of the Mass of the Earth.
PE2 proportional to a3/ME
so (Pmoon/Pspacecraft)2 = (amoon/aspacecraft)3(Mplanet/ME)
Mplanet/ME = (Pmoon/Pplanet)2(aspacecraft/amoon)3
and
Mplanet/ME = (27.3 d/0.202 d)2(100,000 km/384,000 km)3
Mplanet/ME = 322
So the planet is
322 times the mass of the Earth or 322 (6x1024 kg) = 1.9x1027 kg
---------------------------
4-2
Two photons has an energies of 2 and 0.10 electron-volts (eV)
(a) Determine their frequencies, f
(b) Determine their wavelengths, l
-
Photon energy = h f
where h = 6.63x10-34 J.s
and 1 eV = 1.6x10-19 J
wavelength = (speed of light)/frequency
c = 3x108 m/s
Energy Energy(J) frequency wavelength
------ ---------- --------- -----------------
2.0 eV 3.2x10-19 J 4.83x1014Hz 6.21x10-7m = 0.621 micrometres
0.1 eV 0.16x10-19 J 2.41x1013Hz 1.24x10-5m = 12.4 micrometres
---------------------------
4-5
Hydrogen in its third excited state (n = 4)
How many different photons of different wavelength can be emitted in
falling back down to the ground state
See 'More Precisely 4-2 The Energy Levels of the Hydrogen Atom'
n=4 ---------------- E = 12.8eV
n=3 ---------------- E = 12.1eV
n=2----------------- E = 10.2eV
n=1 ---------------- E = 0 eV (ground state)
Transitions can take place as follows with the energy
Transition Energy Wavelength
4 --> 3 0.7 eV 1876.1 nm
4 --> 2 2.6 eV 486.1 nm H(beta)
4 --> 1 12.8 eV 97.3 nm
3 --> 2 1.9 eV 656.3 nm H(alpha)
3 --> 1 12.1 eV 102.6 nm
2 --> 1 10.2 eV 121.6 nm L(alpha)
---------------------------
4-8
Hydrogen gas molecules at 5800 K move on an average of 12 km/s
and doppler shift the Hydrogen alpha line at 656.3 nm. What is the
spectral width of the line.
Calculate the doppler effect due to 12 km/s
dl/l = v/c = (12 km/s)/(300,000 km/s) = 0.000040
dl = 0.000040 (656.3 nm) = 0.026 nm
This is half the width of the line so the thermal width will be
width = 2 dl = 0.052 nm
---------------------------
4-10
Rotation of a Star will also broaden a spectral line. Use the velocity
the molecules in the previous problem to determine the rotation rate of
the Sun to produce the same line boadening.
This means that the surface of the Sun at its equator
would have to move with the velocity of 12 km/s.
Determine what this means in rotational period!
Radius of the Sun = 700,000 km.
velocity = circumference/period
period = [ 2(pi)700,000 km ]/ (12 km/s)
= 366,500 s
= 4.24 days
This is a rotation of 0.24 rotations/day
==============================================================================
Larry Bogan - Oct 19, 1998
-
The wavelength at which the spacecraft is radiating is the average of the
extremes lo = (lred + lblue)/2 as can be
seen from the fact that lred = lo + dl and lblue = lo - dl
Where l = wavelength
dl = diffence in wavelength = apparent wavelength - actual wavelength
lo = 3.000000 m and then dl = 0.00036 m
Using the doppler effect, we can find the velocity of the spacecraft.
v/c = dl/lo
v = 300,000 km/s (0.00036 m/3 m) = 36 km/s
-
The period of the spacecraft orbit is determined from
time (period) = circumference / speed
period = 2 (pi) r /v = 6.28 (100,000 km) / 36 km/s
period = 17453 s = 4.84 hours = 0.202 days
Since this period is more similar to a satellite about the Earth,
let's use the Earth-Moon for Comparison and we will get the mass
of the planet in terms of the Mass of the Earth.
PE2 proportional to a3/ME
so (Pmoon/Pspacecraft)2 = (amoon/aspacecraft)3(Mplanet/ME)
Mplanet/ME = (Pmoon/Pplanet)2(aspacecraft/amoon)3
and
Mplanet/ME = (27.3 d/0.202 d)2(100,000 km/384,000 km)3
Mplanet/ME = 322
So the planet is
322 times the mass of the Earth or 322 (6x1024 kg) = 1.9x1027 kg
---------------------------
4-2
Two photons has an energies of 2 and 0.10 electron-volts (eV)
(a) Determine their frequencies, f
(b) Determine their wavelengths, l
-
Photon energy = h f
where h = 6.63x10-34 J.s
and 1 eV = 1.6x10-19 J
wavelength = (speed of light)/frequency
c = 3x108 m/s
Energy Energy(J) frequency wavelength
------ ---------- --------- -----------------
2.0 eV 3.2x10-19 J 4.83x1014Hz 6.21x10-7m = 0.621 micrometres
0.1 eV 0.16x10-19 J 2.41x1013Hz 1.24x10-5m = 12.4 micrometres
---------------------------
4-5
Hydrogen in its third excited state (n = 4)
How many different photons of different wavelength can be emitted in
falling back down to the ground state
See 'More Precisely 4-2 The Energy Levels of the Hydrogen Atom'
n=4 ---------------- E = 12.8eV
n=3 ---------------- E = 12.1eV
n=2----------------- E = 10.2eV
n=1 ---------------- E = 0 eV (ground state)
Transitions can take place as follows with the energy
Transition Energy Wavelength
4 --> 3 0.7 eV 1876.1 nm
4 --> 2 2.6 eV 486.1 nm H(beta)
4 --> 1 12.8 eV 97.3 nm
3 --> 2 1.9 eV 656.3 nm H(alpha)
3 --> 1 12.1 eV 102.6 nm
2 --> 1 10.2 eV 121.6 nm L(alpha)
---------------------------
4-8
Hydrogen gas molecules at 5800 K move on an average of 12 km/s
and doppler shift the Hydrogen alpha line at 656.3 nm. What is the
spectral width of the line.
Calculate the doppler effect due to 12 km/s
dl/l = v/c = (12 km/s)/(300,000 km/s) = 0.000040
dl = 0.000040 (656.3 nm) = 0.026 nm
This is half the width of the line so the thermal width will be
width = 2 dl = 0.052 nm
---------------------------
4-10
Rotation of a Star will also broaden a spectral line. Use the velocity
the molecules in the previous problem to determine the rotation rate of
the Sun to produce the same line boadening.
This means that the surface of the Sun at its equator
would have to move with the velocity of 12 km/s.
Determine what this means in rotational period!
Radius of the Sun = 700,000 km.
velocity = circumference/period
period = [ 2(pi)700,000 km ]/ (12 km/s)
= 366,500 s
= 4.24 days
This is a rotation of 0.24 rotations/day
==============================================================================
Larry Bogan - Oct 19, 1998
 -
The wavelength at which the spacecraft is radiating is the average of the
extremes lo = (lred + lblue)/2 as can be
seen from the fact that lred = lo + dl and lblue = lo - dl
Where l = wavelength
dl = diffence in wavelength = apparent wavelength - actual wavelength
lo = 3.000000 m and then dl = 0.00036 m
Using the doppler effect, we can find the velocity of the spacecraft.
v/c = dl/lo
v = 300,000 km/s (0.00036 m/3 m) = 36 km/s
-
The period of the spacecraft orbit is determined from
time (period) = circumference / speed
period = 2 (pi) r /v = 6.28 (100,000 km) / 36 km/s
period = 17453 s = 4.84 hours = 0.202 days
Since this period is more similar to a satellite about the Earth,
let's use the Earth-Moon for Comparison and we will get the mass
of the planet in terms of the Mass of the Earth.
PE2 proportional to a3/ME
so (Pmoon/Pspacecraft)2 = (amoon/aspacecraft)3(Mplanet/ME)
Mplanet/ME = (Pmoon/Pplanet)2(aspacecraft/amoon)3
and
Mplanet/ME = (27.3 d/0.202 d)2(100,000 km/384,000 km)3
Mplanet/ME = 322
So the planet is
322 times the mass of the Earth or 322 (6x1024 kg) = 1.9x1027 kg
---------------------------
4-2
Two photons has an energies of 2 and 0.10 electron-volts (eV)
(a) Determine their frequencies, f
(b) Determine their wavelengths, l
-
Photon energy = h f
where h = 6.63x10-34 J.s
and 1 eV = 1.6x10-19 J
wavelength = (speed of light)/frequency
c = 3x108 m/s
Energy Energy(J) frequency wavelength
------ ---------- --------- -----------------
2.0 eV 3.2x10-19 J 4.83x1014Hz 6.21x10-7m = 0.621 micrometres
0.1 eV 0.16x10-19 J 2.41x1013Hz 1.24x10-5m = 12.4 micrometres
---------------------------
4-5
Hydrogen in its third excited state (n = 4)
How many different photons of different wavelength can be emitted in
falling back down to the ground state
See 'More Precisely 4-2 The Energy Levels of the Hydrogen Atom'
n=4 ---------------- E = 12.8eV
n=3 ---------------- E = 12.1eV
n=2----------------- E = 10.2eV
n=1 ---------------- E = 0 eV (ground state)
Transitions can take place as follows with the energy
Transition Energy Wavelength
4 --> 3 0.7 eV 1876.1 nm
4 --> 2 2.6 eV 486.1 nm H(beta)
4 --> 1 12.8 eV 97.3 nm
3 --> 2 1.9 eV 656.3 nm H(alpha)
3 --> 1 12.1 eV 102.6 nm
2 --> 1 10.2 eV 121.6 nm L(alpha)
---------------------------
4-8
Hydrogen gas molecules at 5800 K move on an average of 12 km/s
and doppler shift the Hydrogen alpha line at 656.3 nm. What is the
spectral width of the line.
Calculate the doppler effect due to 12 km/s
dl/l = v/c = (12 km/s)/(300,000 km/s) = 0.000040
dl = 0.000040 (656.3 nm) = 0.026 nm
This is half the width of the line so the thermal width will be
width = 2 dl = 0.052 nm
---------------------------
4-10
Rotation of a Star will also broaden a spectral line. Use the velocity
the molecules in the previous problem to determine the rotation rate of
the Sun to produce the same line boadening.
This means that the surface of the Sun at its equator
would have to move with the velocity of 12 km/s.
Determine what this means in rotational period!
Radius of the Sun = 700,000 km.
velocity = circumference/period
period = [ 2(pi)700,000 km ]/ (12 km/s)
= 366,500 s
= 4.24 days
This is a rotation of 0.24 rotations/day
==============================================================================
Larry Bogan - Oct 19, 1998
-
The wavelength at which the spacecraft is radiating is the average of the
extremes lo = (lred + lblue)/2 as can be
seen from the fact that lred = lo + dl and lblue = lo - dl
Where l = wavelength
dl = diffence in wavelength = apparent wavelength - actual wavelength
lo = 3.000000 m and then dl = 0.00036 m
Using the doppler effect, we can find the velocity of the spacecraft.
v/c = dl/lo
v = 300,000 km/s (0.00036 m/3 m) = 36 km/s
-
The period of the spacecraft orbit is determined from
time (period) = circumference / speed
period = 2 (pi) r /v = 6.28 (100,000 km) / 36 km/s
period = 17453 s = 4.84 hours = 0.202 days
Since this period is more similar to a satellite about the Earth,
let's use the Earth-Moon for Comparison and we will get the mass
of the planet in terms of the Mass of the Earth.
PE2 proportional to a3/ME
so (Pmoon/Pspacecraft)2 = (amoon/aspacecraft)3(Mplanet/ME)
Mplanet/ME = (Pmoon/Pplanet)2(aspacecraft/amoon)3
and
Mplanet/ME = (27.3 d/0.202 d)2(100,000 km/384,000 km)3
Mplanet/ME = 322
So the planet is
322 times the mass of the Earth or 322 (6x1024 kg) = 1.9x1027 kg
---------------------------
4-2
Two photons has an energies of 2 and 0.10 electron-volts (eV)
(a) Determine their frequencies, f
(b) Determine their wavelengths, l
-
Photon energy = h f
where h = 6.63x10-34 J.s
and 1 eV = 1.6x10-19 J
wavelength = (speed of light)/frequency
c = 3x108 m/s
Energy Energy(J) frequency wavelength
------ ---------- --------- -----------------
2.0 eV 3.2x10-19 J 4.83x1014Hz 6.21x10-7m = 0.621 micrometres
0.1 eV 0.16x10-19 J 2.41x1013Hz 1.24x10-5m = 12.4 micrometres
---------------------------
4-5
Hydrogen in its third excited state (n = 4)
How many different photons of different wavelength can be emitted in
falling back down to the ground state
See 'More Precisely 4-2 The Energy Levels of the Hydrogen Atom'
n=4 ---------------- E = 12.8eV
n=3 ---------------- E = 12.1eV
n=2----------------- E = 10.2eV
n=1 ---------------- E = 0 eV (ground state)
Transitions can take place as follows with the energy
Transition Energy Wavelength
4 --> 3 0.7 eV 1876.1 nm
4 --> 2 2.6 eV 486.1 nm H(beta)
4 --> 1 12.8 eV 97.3 nm
3 --> 2 1.9 eV 656.3 nm H(alpha)
3 --> 1 12.1 eV 102.6 nm
2 --> 1 10.2 eV 121.6 nm L(alpha)
---------------------------
4-8
Hydrogen gas molecules at 5800 K move on an average of 12 km/s
and doppler shift the Hydrogen alpha line at 656.3 nm. What is the
spectral width of the line.
Calculate the doppler effect due to 12 km/s
dl/l = v/c = (12 km/s)/(300,000 km/s) = 0.000040
dl = 0.000040 (656.3 nm) = 0.026 nm
This is half the width of the line so the thermal width will be
width = 2 dl = 0.052 nm
---------------------------
4-10
Rotation of a Star will also broaden a spectral line. Use the velocity
the molecules in the previous problem to determine the rotation rate of
the Sun to produce the same line boadening.
This means that the surface of the Sun at its equator
would have to move with the velocity of 12 km/s.
Determine what this means in rotational period!
Radius of the Sun = 700,000 km.
velocity = circumference/period
period = [ 2(pi)700,000 km ]/ (12 km/s)
= 366,500 s
= 4.24 days
This is a rotation of 0.24 rotations/day
==============================================================================
Larry Bogan - Oct 19, 1998