
The following discussion includes only refracting telescopes but it equally applies to reflecting telescopes. We will discuss four properties of the telescope
CONTENTS
The angular size or separation of objects seen in a telescope have values
on the order of minutes and seconds of arc. Thes are small enough that
the skinny triange approximation can be used to calcualte the sizes of
images produced by the telescope given the angular size of the celestial
object.

The relationship d = a D relates the included
angle, a, given in radians with the length,
d,
and the distance, D. (both of the latter must have the same units of length).
There are 2 pi radians in 360 degrees so 1 raidian = 57.3 degrees. Usually we will be discussing images on the order of minutes or seconds of arc so we can convert with 60' arc = 1 degree and 60" arc = 1' arc. This gives 1 radian = 206,300" arc.
It is useful to rewrite the skinny triange as d = (a" D)/(206,300) where a" is the angle in seconds of arc.
Prime Focus is the focus of the objective lens. 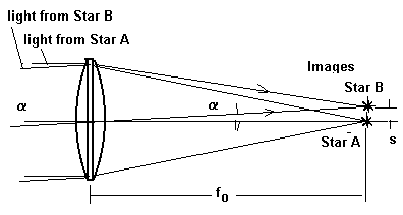
fo = focal length of the objective lens
a = angular separation of the two stars (or
the angular size of an extended object)
(Note: Star A is above Star B in the sky but image of Star B is above that of Star A. This inversion of images is characteristic of astronomical telescopes)
The size of the separation of the images of the two stars represents that on a image detector placed at the prime focus (photographic film or CCD camera).
Size, s = (a" fo)/(206,300)for the angle in " arc. Size, s = (a fo)/57.3 for the angle in degrees.
EXAMPLE:
The Moon's angular size is 31' arc = 31/60 = 0.517degrees
If the focal length of the lens used is 400 mm, then
the diameter of the image produced on film at the prime focus
s = (0.517)(400 mm)/57.3 = 3.6 mm

The apparent angular size of the images as seen through a magnifying
lens is an angle, b. The size of that angle
depends on the focal length of the lens (eyepiece), fe.
Another skinny triange relation give the angle, b
= s/fe .
The magnification, M, is defined as the ratio of the apparent to actual angular separation of the stars.
d/fe
M = b/a = -------- = fe/fo
d/fo
EXAMPLE:
What is the apparent angular size of Mars at opposition (actual angular
size = 26"arc) as seen through the telescope with the following properites:
Objective focal length = 1600 mm
Eyepiece focal length = 25 mm
Magnification = 1600/25 = 64
Apparent angular size of Mars = 64 x 26"arc = 1664"arc = 28'
arc
So in the telescope, Mars will appear about the same size as the Moon is
in the sky.
One of the most important uses of the telescope is to produce a brighter image of celestial object. Some of the objects in the sky are big but too dim to be seen with the eye.
Stars are nearly perfect point objects. Stars are so far away that no matter how much they are magnified, they will always be points of light. (This is not strictly true, of course, since one could not see a true 'point of light'. The images of stars are small, but finite in size. They are produced by the imperfections of the telescope, diffraction, and refraction of a moving atmosphere.)
The amount of light collected by a telescope is proportional to the area of the objective lens.
That area = (pi) D2/4 .
D = diameter of the objective lens.
Since we will not be determining the brightness in absolute flux units
but in terms of relative brightness, we will define the "light gathering
power" in terms of the square of the diameter of the objective.
Ratio of Brightness of the star image of telescope 1 compared with that of telescope 2 is
B1 D12
--- = ------
B2 D22
EXAMPLE:
How many times brighter does a star appear seen through a 5 metre diameter
telescope than that seen by the naked eye (iris diameter = 7 mm).
B1/B2 = (D1/D2)2
= (5000 mm / 7 mm)2 = 510,000
b) Photography of Extended Objects
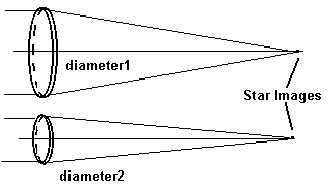
The light from the objective is distributed over the area of the image at prime focus. If the image is made larger by having a larger focal length, then the brightness of the image decreases.

Focal length 2 is longer than focal length 1 and hence image 2 (of the same object) is larger with a larger area. The ratio of the areas of the two images is in proportion to the square of its linear dimensions. This means that the brightness of the image is proportional to the square of the diameter of the objective lens and inversely proportional to the square of the focal length.
B1 (D1/f1)2
---- = -------
B2 (D2/f2)2
The ratio f/D of the focal length to the diameter is defined as the focal ratio = F#
Hence one can write the brightness ratio as:
B1/B2 = (F#2/F#1)2
(Note: This does not apply to visual brightness of two telescopes with the same magnification)
EXAMPLE:
Compare the brightness of the Moon as photographed with two different
telescopes.
a. A Celestron C-8 with diameter = 200 mm and f = 2000 mm (Fa# = 2000/200 = 10)
b. A small 3 inch refractor with Fb# = 8. Diameter = 75 mm. f
= 600 mm.
Ba/Bb = (F#b / F#a)2
= (8/10)2 = 0.64
So the smaller telescope has the brighter image. However, its image
is over 3 times smaller.
Image Size (C-8) = 2000mm(0.5deg/57.3) = 17 mm
Image Size (refractor) = 600mm(0.5/57.3) = 5 mm
Ray optics alone will tell us that a star will be focused to perfect point. However, light is an electromagnetic wave and ray optics ignores the effects of interference of light going trough the lens. Because the lens is not infinite in size, the image of a star will be a finite spot. This is called the diffraction spot. Its size depends on the wavelength of the electromagnetic radiation (light) and the diameter of the objective.
The angular size of the spot (in radians) = q
= 1.2 l/D
l = wavelength, D = diameter
This relationship holds for radio waves as well as light. However, at the moment we are only interested in optical telescopes so we will pick l = 550 nm. Telescopes with larger diameter objectives have diffraction spots that are smaller.
q ("arc) = 138 /D(mm)

Two stars can be resolved into the pair only if they are farther apart than the diameter of the diffraction spots produced by the telescope. Likewise, an extended object can be resolved only if the resolution of the telescope is smaller than the angular size of the object.
Example:
What minimum diameter of a telescope is necessary to resolve a 1 km
diameter crater on the Moon?
First calculate the angular size that 1 km on the Moon appears at the Earth.
Distance to the Moon = 384,000 km 1 radian = 206,300"arc
Use the skinny triange: a" = [1 km/384,000km
]206,300"/rad = 0.54" arc
So we need to resolve 0.54"arc to see a 1km diameter crater.
D(mm) = 138/a" = 138/0.54 = 257 mm
A 33 cm telescope would theoretically be able to resolve a 1 km crater
on the Moon. The difficulty is that refraction of the atmosphere of the
Earth generally distorts the image such that nothing smaller than 1"
arc can be seen. It is only on very rare nights that 0.5"arc seeing
is available.
The eye does not respond linearly to the brightness of an object. This means that a star twice a bright does not induce twice the response but actually less. The dependence is logrithmic. An example is that if there are three stars A, B, and C with brightness 1, 2 and 4, the response of the eye is 0, 1, 2 not 1, 2, 4.
Historically, the magnitude scale for the stars was established thousands of years ago and the modern system is based on it. The relationship is established by defining a difference of 5 magnitudes as being equal to a ratio of 100 in brightness. Note that the magnitude scale step linearly while the brightness scale is geometrical (deals with ratios). 1 magnitude difference equals a ratio of brightness of 2.51.
The mathematical formula that relates relative magnitudes, m, to relative brightness, B, is: m2 corresponds to B2 while m1 corresponds to B1
m2 - m1 = 2.5 log10(B1/B2)
Note that when B1 is greater than B2, then m2 is greater than m1.
This formula can be rearranged to obtain brightness ratios
from magnitude differences
B1/B2 =100.4 (m2 - m1)
Table of magnitude differences:
m2 - m1 B1/B2
--------- -------
0.1 1.096
0.2 1.202
0.3 1.318
0.4 1.445
0.5 1.585
0.6 1.738
0.7 1.905
0.8 2.089
0.9 2.290
1.0 2.511
2.0 (2.511)2 = 6.31
3.0 (2.511)3 = 15.85
4.0 (2.511)4 = 39.81
5.0 (2.511)5 = 100
Example 1:
Find the ratio of brightness of two stars whose magnitudes we know.
Rigel (beta Orionis)= 0.12 m
delta Orionis = 2.23
Find the ratio in brightness
magnitude difference = 2.23 - 0.12 = 2.11 ~ 2.1
2 magnitudes = ratio of 6.31
0.1 magnitudes = ratio of 1.096
So the brightness ratio = 6.31 x 1.096 = 6.9
Example 2:
Find the magnitude difference of two stars when their brightness ratio
has been determined by a photometer.
Ratio of brightness measured by photometer = 1256
What is the difference in the magnitudes? First break the ratio up into
factors that match the magnitude difference in the table.
1256 = 100 x 12.56 = 100 x 6.31 x 1.99
The corresponding magnitude differences for the ratios
100 --> 5 mag
6.31 --> 2 mag
1.99 --> 0.75 mag
difference in magnitudes = 5 + 2 + 0.75 = 7.75
Alternately use the formula
m2 - m1 = 2.5 log10(B1/B2)
m2 - m1 = 2.5 log10(1256) = 2.5 (3.10) = 7.75
Example 3:
What effect does adding together many different magnitudes such as we might
have in a star cluster?
An open cluster is made of 30, 13th magnitude stars
What is the total magnitude of the cluster.
Cluster is 30 times brighter that one star.
break up 30 = 15.9 x 1.89
15.9 = 3 mag
1.89 = 0.7 mag
So the cluster has the magnitude of 13 - 3 - 0.7 = 9.3 m
Alternately use the formula
m2 = star, m1 = cluster
m2 - m1 = 2.5 log10(B1/B2)
m2 - m1 = 2.5 log10(30) = 2.5 (1.477) = 3.69
m1 = m2 - 3.69 = 13 - 3.6 = 9.31
NOTE: The whole cluster has a magnitude smaller than that of a single star in the cluster.