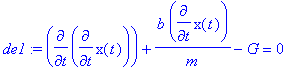
>

The following statement defines the differential equation which we wish to solve. To clean

up the code, I have introduced the variable G=g(sin(theta)-mu_k*cos(theta)) To clean up the equation.

> de1 := diff(x(t),t$2) + b/m*diff(x(t),t) -G = 0;

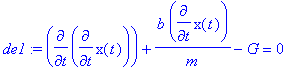
We now solve the above equation, subject to the boundary conditions that both the position and velocity must be equal to zero at time t=0

> ### WARNING: `dsolve` has been extensively rewritten, many new result forms can occur and options are slightly different, see help page for details
dsolve({de1, x(0)=0, D(x)(0)=0}, x(t),method=laplace);

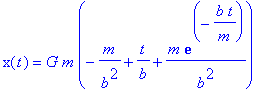
Define the position function with the solution obtained above

> y(t):=G*m*(-m/b^2+t/b+m*exp(-b*t/m)/b^2);

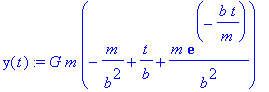
Differentiate position with respect to time to get velocity

> v:=diff(y(t),t);

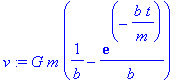
Differentiate velocity with respect to time to get acceleration

> a:=diff(v,t);

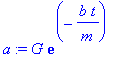
> b:=1;G:=9.8;m:=50;

> plot(y(t),t=0..200);

> plot(v,t=0..200);

> plot(a,t=0..200);

>