Astronomy 1 - Physics 1513
Monday Oct 26, 1998
Overview of Solar System
ASTRONOMICAL EVENT:
Orionid Meteors (last Thursday) Duration 8 days, peak 20/hr, speed 66 km/s
HOMEWORK:
Telescopes (See Optics Page)
See Assignment #7 on Acme
LECTURE
1. Layout and Components of the Solar System
History of Discovery
Pre-History (Sun, Mercury, Moon, Venus, Mars, Jupiter, Saturn)
Each planet had a day of the week
In order of supposed decreasing distance from the Earth
(The slower moving were considered farther away -
in reality Mercury is farther away than Venus)
Each hour of the day (24) were governed by a planet and the
one that governed the first hour governed the day.
Sat Jup Mars Sun Ven Merc Moon
Sat 1 2 3 4 5 6 7
8 9 10 11 12 13 14
15 16 17 18 19 20 21
Sun 22 23 24 1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
Moon 19 20 21 22 23 24 1
2 3 - - -
Mars 23 24 1 2 - -
Mercury - - - 23 24 1 2
Jupiter 24 1 - - - -
Venus - - 23 24 1 2 -
Italian Anglo
Names Saxon
------- ------
Saturday Saturn
Sunday Sun
Monday Moon
Tuesday Mars Martedi
Wednesday Mercury Mercoledi Odin's Day
Thursday Jupiter Giovedi Thunder Day
Friday Venus Venerdi Frigga's Day
History of Planetary and Satellited Discoveries
Satellites of Jupiter [Galileo, 1609]
Rings of Saturn [Cassini, 1659]
Uranus [Sir William Hershel (Britian - 1758)]
Ceres [Piazzi in Italy, 1801]
- Lost - Gauss's orbit found 1 year later
Neptune
[predicted by Adams and Leverrier
Discover by Galle in Germany 1846]
Pluto [Clyde Tombaugh, USA, 1930]
Present Positons of Planets (Use ECU)
Heliocentric and Geocentric Longitudes (Nov 1, 1998)
Heliocentric Longitude = angle centred on the Sun of the
planet from vernal equinox
Elongation from the Sun = angle centred on the Earth of
the planet from the Sun
Geocentric Longitude = angle centred on Earth of the
planet from the vernal equinox
DIAGRAM of Longitude and Elongation Definitions
----------------------- Positions at November 1, 1998 ----------------
Helio Magnitude Rate Period
360deg/period years)
----- ----- ----- -----
Mercury 292 -0.2 4.09 0.241
Venus 219 -3.9 1.60 0.615
Earth 38 0.986 deg/day 1.00
Mars 136 1.6 0.524 deg/day 1.88
Ceres 7.4
Vesta 7.9
Jupiter 357 -2.7 30.35 deg/year 11.86
Saturn 30 -0.2 12.2 29.42
Uranus 312 5.8 4.3 83.75
Neptune 201 7.9 2.2 163.7
Pluto 248 13.7 1.45 248.0
DIAGRAM showing Positions of Planets in Orbits for November 1, 1998
Titus-Bode Law Johann Titus(1766)
n 0.3[2(n-1)] + 0.4 actual
---------- ----- -----
Mercury - 0.4 n not used 0.39
Venus 1 0.7 0.72
Earth 2 1.0 1.00
Mars 3 1.6 1.52
-- 4 2.8 Ceres (2.8)
Jupiter 5 5.2 5.2
Saturn 6 10.0 9.5
Uranus 7 19.6 19.2
Neptune 8 38.8 30.1
Pluto 9 77.2 39.5
Size, Density, Composition
Dia Mass Density Period
(km) M(earth) (days)
-------- ----- ---- --- Rotation P(d)
Terrestial
Mercury 4900 0.055 5.4 59
Venus 12100 0.82 5.2 243(retrograde)
Earth 12800 1.0 5.5 1.0
Moon 3500 0.012 3.3 27.3
Mars 6800 0.107 3.9 1.03
Ceres 1000 2.7
Jovian
Jupiter 143,000 318 1.3 0.41
Saturn 120,500 95.2 0.7 0.44
Uranus 51,100 14.5 1.2 0.71
Neptune 49,500 17.2 1.7 0.67
Pluto 2300 0.003 2.0 6.4
Comets and Asteroids
Places, Composition, and density
Space Probes
Orbits of a transfer orbit
Example: Space Probe to Venus - later
Mercury
1974 Mariner 10 in 176 day period (twice siderial period of Mercury)
45% of surface imaged
Venus
1962 Mariner 2
1967 Mariner 5
1974 Mariner 10
1967-78 Venera 4-12 (1970 Venera 7 soft-landing)
1983 Venera 15-16 orbiters
1978 Pioneer Venus mapped surface
1990 Magellan (mapped detail 120m size)
Mars
1965 Mariner 4
1969 Mariner 6, 7
1971 Mariner 9 orbiter mapped to 1 km size
1976 Viking 1 and 2 orbiter and landers
(tests for life and pictures of surface)
1997 Mars Sojourner and Global Explorer (orbiter)
1999 Mars Surveyor Lander
Jupiter
1972 Pioneer 10
1973 Pioneer 11
1979 Voyageur 1
1979 Voyageur 2
1995 Galileo (Probe into atmosphere and orbiter)
Saturn
1980 Voyager 1
1981 Voyager 2
2004 Cassini (Earth gravity assist in 1999)
Uranus
1986 Voyager 2
Neptune
1989 Voyager 2
Comets
1986 Vega 2 and Giotto flyby of Halley
Asteroids
Galileo (Imaged Gaspra and Ida)
Near on its way to Eros (imaged Mathilda)
Orbital Transfer of Space Probe from Earth to Venus
 Use rper = a(1-e)
raph = a(1+ e)
e = ra/a - 1
a = (ra + rp)/2
P2 = a3
vcircular = 2(pi)a/P gives the relationship v ~ a-1/2
= (MG/a)1/2
Use a mathematical form of Kepler's 2nd Law:
vprp = vara
to get
vp = vc[(1+e)/(1-e)]1/2
and
va = vc[(1- e)/(1+ e)]1/2
Earth Venus Venus Probe
----- ------ -----------
Semi-major axis 1.00 0.723 AU 0.861
Orbit Period 365.25 224.7 days 292 days (Travel time = 292/2 = 149 days)
Orbit Velocity 29.8 35.0 km/s 32.1(average)
Orbit Eccentricity 0.016 0.007 0.15
Velocity at aphelion 27.6 km/s (at Launch, Earth)
" perihelion 37.3 km/s (at Arrival, Venus)
Longitude at Launch 0 -54 deg 0
Longitude at Arrival 144 180 180
Solar Orbit speed at Earth must be reduced by 2.2 km/s to be sent to Venus
Solar Orbit speed at Venus must be reduced by 2.3 km/s to match Venus' orbital speed.
Sphere of Influence and the Slingshot Effect
The sphere of influence of Venus depends on its mass relative
to that of the Sun and its distance to the Sun.
Radius of Sphere = (0.723 AU) [M(venus)/M(sun)]2/5
= 620,000 km =102 R(Venus)
Outside the sphere:
The orbit is around the Sun - Elliptical (velocity = 37.3 km/s)
Inside the sphere of influence:
The orbit is around Venus - Hyperbolic (velocity = 2.3 km/s)
If the space probe enters the Venus sphere of influence
at 45 degrees outside the orbit and with its velocity
parallel to that of Venus then:
Hyperbolic Orbit semi-major axis = a = 76,900 km
closest approach to Venus = 419,000 km
eccentricity = 6.45
Angle centered on Venus:
51.3 degrees from entry of sphere to closest approach
As the probe enters the sphere of influence with 2.3 km/s,
it also leaves the sphere with the same speed but with a
different direction. (different velocity)
Outside: Leave with velocity component toward the Sun (0.5 km/s)
angle of velocity with respect to Venus' is 12.6 degrees
The net velocity relative to the Sun is slightly lower at 37.25 km/s
If the probe had entered the sphere of influence at a greater angle
the change in speed would be greater. Also if it went closer to Venus
it would change more.
Use rper = a(1-e)
raph = a(1+ e)
e = ra/a - 1
a = (ra + rp)/2
P2 = a3
vcircular = 2(pi)a/P gives the relationship v ~ a-1/2
= (MG/a)1/2
Use a mathematical form of Kepler's 2nd Law:
vprp = vara
to get
vp = vc[(1+e)/(1-e)]1/2
and
va = vc[(1- e)/(1+ e)]1/2
Earth Venus Venus Probe
----- ------ -----------
Semi-major axis 1.00 0.723 AU 0.861
Orbit Period 365.25 224.7 days 292 days (Travel time = 292/2 = 149 days)
Orbit Velocity 29.8 35.0 km/s 32.1(average)
Orbit Eccentricity 0.016 0.007 0.15
Velocity at aphelion 27.6 km/s (at Launch, Earth)
" perihelion 37.3 km/s (at Arrival, Venus)
Longitude at Launch 0 -54 deg 0
Longitude at Arrival 144 180 180
Solar Orbit speed at Earth must be reduced by 2.2 km/s to be sent to Venus
Solar Orbit speed at Venus must be reduced by 2.3 km/s to match Venus' orbital speed.
Sphere of Influence and the Slingshot Effect
The sphere of influence of Venus depends on its mass relative
to that of the Sun and its distance to the Sun.
Radius of Sphere = (0.723 AU) [M(venus)/M(sun)]2/5
= 620,000 km =102 R(Venus)
Outside the sphere:
The orbit is around the Sun - Elliptical (velocity = 37.3 km/s)
Inside the sphere of influence:
The orbit is around Venus - Hyperbolic (velocity = 2.3 km/s)
If the space probe enters the Venus sphere of influence
at 45 degrees outside the orbit and with its velocity
parallel to that of Venus then:
Hyperbolic Orbit semi-major axis = a = 76,900 km
closest approach to Venus = 419,000 km
eccentricity = 6.45
Angle centered on Venus:
51.3 degrees from entry of sphere to closest approach
As the probe enters the sphere of influence with 2.3 km/s,
it also leaves the sphere with the same speed but with a
different direction. (different velocity)
Outside: Leave with velocity component toward the Sun (0.5 km/s)
angle of velocity with respect to Venus' is 12.6 degrees
The net velocity relative to the Sun is slightly lower at 37.25 km/s
If the probe had entered the sphere of influence at a greater angle
the change in speed would be greater. Also if it went closer to Venus
it would change more.
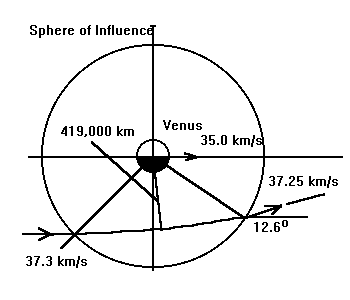 DIAGRAM showing velocity vector for slingshot effect
--------------------------------------------------------------------
WHY AIR STICKS to the PLANETS 'More Precisely 8-1' (Page 180-181)
Discuss the Dynamics of Atmospheres on Planets (Thermal Velocity and Escape Velocity)
DIAGRAM showing velocity vector for slingshot effect
--------------------------------------------------------------------
WHY AIR STICKS to the PLANETS 'More Precisely 8-1' (Page 180-181)
Discuss the Dynamics of Atmospheres on Planets (Thermal Velocity and Escape Velocity)
 Use rper = a(1-e)
raph = a(1+ e)
e = ra/a - 1
a = (ra + rp)/2
P2 = a3
vcircular = 2(pi)a/P gives the relationship v ~ a-1/2
= (MG/a)1/2
Use a mathematical form of Kepler's 2nd Law:
vprp = vara
to get
vp = vc[(1+e)/(1-e)]1/2
and
va = vc[(1- e)/(1+ e)]1/2
Earth Venus Venus Probe
----- ------ -----------
Semi-major axis 1.00 0.723 AU 0.861
Orbit Period 365.25 224.7 days 292 days (Travel time = 292/2 = 149 days)
Orbit Velocity 29.8 35.0 km/s 32.1(average)
Orbit Eccentricity 0.016 0.007 0.15
Velocity at aphelion 27.6 km/s (at Launch, Earth)
" perihelion 37.3 km/s (at Arrival, Venus)
Longitude at Launch 0 -54 deg 0
Longitude at Arrival 144 180 180
Solar Orbit speed at Earth must be reduced by 2.2 km/s to be sent to Venus
Solar Orbit speed at Venus must be reduced by 2.3 km/s to match Venus' orbital speed.
Sphere of Influence and the Slingshot Effect
The sphere of influence of Venus depends on its mass relative
to that of the Sun and its distance to the Sun.
Radius of Sphere = (0.723 AU) [M(venus)/M(sun)]2/5
= 620,000 km =102 R(Venus)
Outside the sphere:
The orbit is around the Sun - Elliptical (velocity = 37.3 km/s)
Inside the sphere of influence:
The orbit is around Venus - Hyperbolic (velocity = 2.3 km/s)
If the space probe enters the Venus sphere of influence
at 45 degrees outside the orbit and with its velocity
parallel to that of Venus then:
Hyperbolic Orbit semi-major axis = a = 76,900 km
closest approach to Venus = 419,000 km
eccentricity = 6.45
Angle centered on Venus:
51.3 degrees from entry of sphere to closest approach
As the probe enters the sphere of influence with 2.3 km/s,
it also leaves the sphere with the same speed but with a
different direction. (different velocity)
Outside: Leave with velocity component toward the Sun (0.5 km/s)
angle of velocity with respect to Venus' is 12.6 degrees
The net velocity relative to the Sun is slightly lower at 37.25 km/s
If the probe had entered the sphere of influence at a greater angle
the change in speed would be greater. Also if it went closer to Venus
it would change more.
Use rper = a(1-e)
raph = a(1+ e)
e = ra/a - 1
a = (ra + rp)/2
P2 = a3
vcircular = 2(pi)a/P gives the relationship v ~ a-1/2
= (MG/a)1/2
Use a mathematical form of Kepler's 2nd Law:
vprp = vara
to get
vp = vc[(1+e)/(1-e)]1/2
and
va = vc[(1- e)/(1+ e)]1/2
Earth Venus Venus Probe
----- ------ -----------
Semi-major axis 1.00 0.723 AU 0.861
Orbit Period 365.25 224.7 days 292 days (Travel time = 292/2 = 149 days)
Orbit Velocity 29.8 35.0 km/s 32.1(average)
Orbit Eccentricity 0.016 0.007 0.15
Velocity at aphelion 27.6 km/s (at Launch, Earth)
" perihelion 37.3 km/s (at Arrival, Venus)
Longitude at Launch 0 -54 deg 0
Longitude at Arrival 144 180 180
Solar Orbit speed at Earth must be reduced by 2.2 km/s to be sent to Venus
Solar Orbit speed at Venus must be reduced by 2.3 km/s to match Venus' orbital speed.
Sphere of Influence and the Slingshot Effect
The sphere of influence of Venus depends on its mass relative
to that of the Sun and its distance to the Sun.
Radius of Sphere = (0.723 AU) [M(venus)/M(sun)]2/5
= 620,000 km =102 R(Venus)
Outside the sphere:
The orbit is around the Sun - Elliptical (velocity = 37.3 km/s)
Inside the sphere of influence:
The orbit is around Venus - Hyperbolic (velocity = 2.3 km/s)
If the space probe enters the Venus sphere of influence
at 45 degrees outside the orbit and with its velocity
parallel to that of Venus then:
Hyperbolic Orbit semi-major axis = a = 76,900 km
closest approach to Venus = 419,000 km
eccentricity = 6.45
Angle centered on Venus:
51.3 degrees from entry of sphere to closest approach
As the probe enters the sphere of influence with 2.3 km/s,
it also leaves the sphere with the same speed but with a
different direction. (different velocity)
Outside: Leave with velocity component toward the Sun (0.5 km/s)
angle of velocity with respect to Venus' is 12.6 degrees
The net velocity relative to the Sun is slightly lower at 37.25 km/s
If the probe had entered the sphere of influence at a greater angle
the change in speed would be greater. Also if it went closer to Venus
it would change more.
 DIAGRAM showing velocity vector for slingshot effect
--------------------------------------------------------------------
WHY AIR STICKS to the PLANETS 'More Precisely 8-1' (Page 180-181)
Discuss the Dynamics of Atmospheres on Planets (Thermal Velocity and Escape Velocity)
DIAGRAM showing velocity vector for slingshot effect
--------------------------------------------------------------------
WHY AIR STICKS to the PLANETS 'More Precisely 8-1' (Page 180-181)
Discuss the Dynamics of Atmospheres on Planets (Thermal Velocity and Escape Velocity)